O que é cálculo integral?

Em Ferramentas por André M. Coelho

As integrais são uma das partes essenciais do cálculo, sendo essenciais para diversas fórmulas e o desenvolvimento das mais diversas e complexas teorias. Entendê-las é papel de qualquer estudante de exatas para progredir no aprendizado do cálculo. Vamos explicar a teoria e a prática das integrais no aprendizado das exatas.

O que é integral?

Uma integral é um objeto matemático que pode ser interpretado como uma área ou uma generalização de área. Integrais, juntamente com derivadas, são os objetos fundamentais do cálculo. Outras palavras para integral incluem antiderivativa e primitiva.

Integral de Riemann

A integral de Riemann da função f (x) sobre x de a a b é escrita da seguinte maneira:

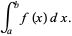
Integral de Riemann

Observe que se f (x) = 1, a integral é escrita simplesmente

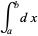
Riemann simplificada

Toda definição de uma integral é baseada em uma medida específica. Por exemplo, a integral de Riemann é baseada na medida de Jordan e a integral de Lebesgue é baseada na medida de Lebesgue.

Integral de Lebesque

Além disso, dependendo do contexto, qualquer uma de uma variedade de outras notações integrais pode ser usada. Por exemplo, a integral de Lebesgue de uma função integrável f sobre um conjunto X mensurável em relação a uma medida μ é frequentemente escrita:

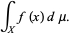
Integral de Lebesque

Caso o conjunto X in () seja um intervalo X = [a, b], a notação “subscrito-sobrescrito” da integral de Riemann simplificada é geralmente adotada.

Integral de Stieltjes

Outra generalização da integral de Riemann é a integral de Stieltjes, onde a função integrando f definida em um intervalo fechado I = [a, b] pode ser integrada contra uma função limitada de valor real alfa (x) definida em I, cujo resultado é o tem a forma

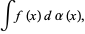
Integral de Stieltjes

Ou de forma equivalente:

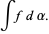
Integral equivalente de Stieltjes

Notações equivalentes de integrais

Ainda outro cenário no qual a notação pode mudar ocorre no estudo da geometria diferencial, através do qual o integrando f (x) dx é considerado um diferencial geral de forma k Ω = f (x) dx e pode ser integrado em um conjunto X usando uma das notações equivalentes

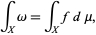
Integral de notação equivalente

Onde μ é a medida de Lebesgue acima mencionada. Vale a pena notar que a notação no lado esquerdo da equação () é semelhante à da expressão () acima.

O cálculo integral pode auxiliar a encontrar diversos resultados importantes, e não é tão difícil quanto possa parecer. (Foto: Medium)

Fórmulas de integrais

O processo de computar uma integral é chamado integração (um termo mais arcaico para integração é quadratura), e o cálculo aproximado de uma integral é denominado integração numérica.

Existem duas classes de integrais (Riemann): que possuem limites superior e inferior, e integrais indefinidas, como

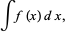
Integral indefinida

Que são escritos sem limites. O primeiro teorema fundamental do cálculo permite que integrais definidas sejam computadas em termos de integrais indefinidas, pois se F (x) é a integral indefinida de f (x), então:

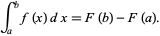
Teorema fundamental do cálculo

Além disso, o primeiro teorema fundamental do cálculo pode ser reescrito de maneira mais geral em termos de formas diferenciais (como em () acima) para dizer que a integral de uma forma diferencial ômega sobre o limite ∂ω de alguma variedade orientável ω é igual ao exterior dω derivada de ω sobre o interior de ω, ou seja,

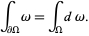
Primeiro teorema fundamental do cálculo

Escrito nesta forma, o primeiro teorema fundamental do cálculo é conhecido como Teorema de Stokes.

Como a derivada de uma constante é zero, integrais indefinidas são definidas apenas até uma constante arbitrária de integração C, ou seja,

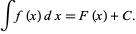
Integral indefinida

Diferenciação de integrais

A diferenciação de integrais leva a algumas identidades úteis e poderosas. Por exemplo, se f (x) for contínuo, então

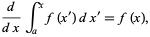
Diferenciação de integrais

Qual é o primeiro teorema fundamental do cálculo. Outras identidades derivadas-integrais incluem:

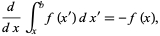
Identidade integral derivada

A regra integral de Leibniz

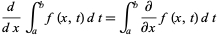
Regra integral de Leibniz

Sua generalização

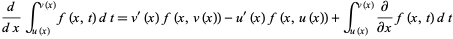
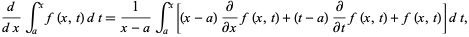
Generalização de Leibniz

Existem dezenas de outras identidades integrais que devem ser usadas para o cálculo e simplificação das fórmulas.

Como calcular integral?

Você pode usar calculadoras online para fazer o cálculo das integrais sem muita dificuldade, com os passos que foram realizados para o cálculo completo da integral, inclusive. Calculadoras científicas e mais avançadas também permitem a integração.

Etapa 1: encontrar uma derivada

Encontre ou crie uma função para uma variável. A função fornecerá uma saída que podemos usar como a segunda variável em um gráfico bidimensional, que na maioria dos casos significa f (x) = y.

Use o quociente de diferença de Newton. Para um pequeno segmento de um gráfico de funções, com largura h, a inclinação é encontrada com m = [f (x + h) -f (x)] / h, assumindo o limite dessa equação em h se aproxima de 0.

Elabore a matemática. No polinômio de exemplo, substituímos todas as instâncias de (x) por (x + h) para obter m = [2 (x + h) ^ 3 + 4 (x + h) ^ 2 +3 (x + h) + 5 – 2x ^ 3 – 4x ^ 2 – 3x – 5] / h. Isso funciona para m = 6x ^ 2 + 6xh + 8x + 2h ^ 2 + 4h + 3, quando h se aproxima de 0. Assim, a inclinação da expressão 2x ^ 3 + 4x ^ 2 + 3x + 5 é dada em qualquer x valor de 6x ^ 2 + 8x + 3. A maioria das pessoas que estuda derivadas pela primeira vez achará útil calcular totalmente a álgebra. Se você ainda luta, pode encontrar orientações passo a passo com um tutor ou em calculadoras online.

Generalize os resultados para encontrar regras de derivação. Como você pode observar no exemplo anterior, o expoente de cada termo diminui em um no polinômio derivado; existem regras derivadas exibidas acima para alguns casos gerais que foram estudados várias vezes.

Etapa 2: soma de Riemann

Encontre uma função cujas coordenadas (x, y) você possa calcular ao longo de um intervalo. Intervalos comuns geralmente começam em ou centram-se em torno de x = 0.

Divida a área sob a curva em segmentos retangulares razoavelmente pequenos de largura uniforme. Por exemplo, 0,1x unidades separadas.

Aproxime a altura de cada segmento com o valor y da função a meio caminho entre seus valores alto e baixo x. Em algumas circunstâncias, você pode querer especificamente uma aproximação estritamente muito alta ou muito baixa, solicitando que você use um valor y diferente do segmento da curva.

Encontre a área de cada segmento multiplicando a altura pela largura. Você precisará registrar essas áreas individuais para a próxima etapa.

Adicione as áreas para encontrar a área total sob a curva do intervalo. Essa é uma grande quantidade de trabalho matemático, mas é confiável e quase se aproxima da área total, especialmente com segmentos mais estreitos. É assim que a maioria das calculadoras executa integrais.

Etapa 3: Integração Definida

Encontre um polinômio simples, como os das etapas anteriores.

Encontre uma regra de derivação que possa produzir a função. Como existem vários tipos de funções e exemplos infinitos para cada tipo, além de combinações de tipos, além de algumas funções impossíveis de integrar, não é possível explorar exaustivamente as opções de integração; neste caso, a resposta deve ser direta.

Inverta o processo de uma derivação. Para um termo polinomial, aumente o expoente em um e divida o coeficiente pelo novo expoente.

Considere uma constante de integração. Quando você encontra a derivada de um polinômio que fornece y em função de x, o termo final, que está no poder de x ^ 0, é perdido. Um determinado derivado polinomial pode vir de um número infinito de polinômios parentais. No entanto, todas as coordenadas são deslocadas pela mesma constante, portanto a próxima etapa ainda funciona.

Encontre a diferença entre as extremidades da função integrada. Como a função original, a derivada dessa nova função, fornece a série de slops entre essas extremidades, essa diferença é igual à área sob a curva da função original. Esse relacionamento é amplamente pouco intuitivo; portanto, tente elaborar quantos exemplos forem necessários para observá-lo.

Ficou alguma dúvida? Deixem nos comentários suas perguntas e iremos ajudar nos estudos em matemática!

Sobre o autor

Engenheiro eletricista, André sempre foi interessado em novas tecnologias. Na primeira década dos anos 2000, atuou como consultor tecnológico em empresas, ajudando as empresas a escolherem as melhores tecnologias para suas necessidades. Desde então, continuou estudando o assunto e hoje compartilha o que aprendeu e continua aprendendo através do site Tecnologia É.

Veja também